[PRML] 1.4 The Curse of Dimensionality

1.4 The Curse of Dimensionality

 

앞서 살펴본 다항 곡선 피팅 예제에서는 입력 데이터 $x$가 단 한 개였다.

그러나 현실 세계의 패턴 인식에서는 높은 차원의 입력 데이터를 다뤄야 하는 경우가 잦다.

이 장에서는 높은 차원의 데이터를 다루며 마주치게 되는 문제들에 대해서 이야기하겠다.

 

Figure 1.19 차원의 저주 예제

문제를 설명하기 위해 기름, 물, 가스가 혼합된 파이프에서 측정한 값을 나타내는 데이터 셋을 고려한다.

그림 1.19는 이 데이터 세트의 측정치 중 $x_6$과 $x_7$ 두 가지를 나타낸다.

각 데이터 포인트는 homogenous, annular, laminar 중 하나의 레이블을 가지고 있으며, 이 레이블은 그림에서 색깔로 분류된다.

우리의 목표는 새로운 데이터 포인트(그림의 x)가 주어졌을 때 이것을 기름, 물, 가스 중 하나로 분류하는 것이다.

 

하나의 간단한 방법은 그림 1.20에서처럼 입력 공간을 균일한 셀(cell)로 나누어, 각 셀에서 가장 많이 등장한 클래스를 해당 셀의 클래스로 생각하는 방법이다.

이 방법에서 새로운 데이터 포인트 x가 속한 셀에는 빨간색 점이 가장 많으므로, x가 속한 클래스는 homogenous라고 예측할 수 있다.

 

 

Fig 1.20 셀 나누기 방법

이 간단한 방법에는 여러가지 문제가 있지만, 그 중의 가장 심각한 문제는 입력 공간의 차수가 높아질수록 두드러진다.

그림 1.21을 보면 입력 공간을 균일한 셀로 나눌 때, 공간의 차수가 증가할수록 셀의 수는 지수적으로 증가한다는 것을 알 수 있다.

셀이 많아질 경우 생길 수 있는 문제점은 각 셀을 채우기 위해 마찬가지로 지수적으로 많은 학습 데이터가 필요하다는 것인데, 이는 불가능하므로 조금 더 정교한 방법이 필요함을 알 수 있다.

 

Figure 1.21 데이터의 차원에 따라 증가하는 셀 개수

 

---

 

다시 다항 곡선 피팅 예제로 돌아가자.

만약 입력값의 차수가 $D$개라면, 차수가 3인 결정 함수는 다음의 형태로 주어진다.

 

$y(\mathbb{x}, \mathbb{w}) = w_0 + \sum_{i=1}^D w_i x_i + \sum_{i=1}^D \sum_{j=1}^D w_{ij}x_ix_j + \sum_{i=1}^D\sum_{j=1}^D\sum_{k=1}^Dw_{ijk}x_ix_jx_k$

 

이러한 방식을 채택한다면 차수가 $M$인 다항 함수를 학습시키기 위해 결정해야 할 계수의 개수는 $D^M$에 비례하게 된다.

 

---

 

이러한 문제를 기하학적으로 살펴보자.

반지름의 길이가 $r$인 구의 $D$차원에서의 부피는 다음과 같이 주어진다.

 

$V_D(r) = K_Dr^d$

 

그렇다면 반지름의 길이가 $1$인 구에서 반지름의 길이가 $1-\epsilon$인 구를 빼 껍질 형태의 도형을 얻는다면, 초기 구의 부피와 도형의 부피비는 다음과 같을 것이다.

 

 $\frac{V_D(1) - V_D(1-\epsilon)}{V_D(1)} = 1 - (1-\epsilon)^D$

 

$D$의 값이 커질수록 무척 작은 $\epsilon$값이라 할지라도, 이 비율이 거의 1에 가까워지는 것을 관찰할 수 있다.

즉, 차원이 증가할수록 구의 부피의 대부분이 껍질에 위치한다.

Figure 1.22 $\epsilon$과 $D$의 변화에 따른 구의 껍질과 구의 부피비 변화

 

---

 

패턴 인식과 조금 더 직접적인 관련성을 가진 예로서, 다차원 공간에서의 가우시안 분포를 생각해 볼 수 있다.

데카르트 좌표계를 극좌표로 변환하고 방향 변수를 통합하면 결국 원점으로부터 각 데이터포인트까지의 거리를 얻을 수 있다.

이 때 $D=1$에서의 가우시안 분포는 우리에게 친숙한 모양을 가지고 있지만,

고차원에서는 위의 구 예제와 같이 거리의 평균이 점점 바깥쪽으로 이동하는 것을 볼 수 있다.

 

 

---

 

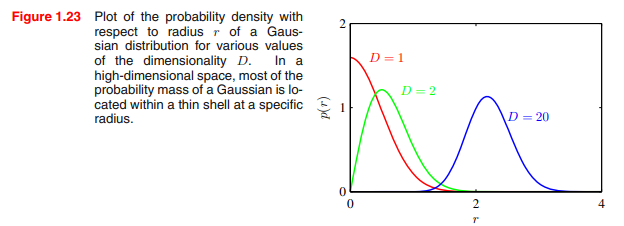
고차원 공간에서 발생할 수 있는 어려움들을 차원의 저주(curse of dimensionality)라고 한다.

책에서는 시각화 등의 이유로 1차원이나 2차원의 예제들을 자주 사용하지만, 독자는 저차원에서의 직관이 고차원에서 그대로 통용될 것이라고 생각하면 안 된다.

 

차원의 저주가 패턴 인식에 있어 여러 문제제기를 가능하게 한다.

하지만 고차원 공간에서 통용될 수 있는 기법들을 찾을 수 없다는 뜻은 아닌데, 그 이유는 다음과 같다.

• 실제 데이터는 종종 모든 변수가 아닌 중요한 몇몇 변수들에 종속될 것이다.
• 실제 데이터는 일반적으로 (적어로 부분적으로는) 평활(smoothness) 속성을 나타낼 것이다.
  • 입력 변수의 작은 변화가 타겟 변수의 작은 변화를 만든다
  • 새로운 입력 변수에 대해 local interpolation과 같은 기법을 사용하여 예측할 수 있다.

예를 들어 컨베이어 벨트에서 촬영된 사물들의 사진을 보고 사물들의 방향을 확인하고자 한다고 하자.

각 이미지는 고차원 공간의 한 점으로 표현될 수 있다.

개체들이 이미지 내에서 서로 다른 방향과 위치에 존재할 수 있기 때문에, 각 이미지들은 3차원의 자유도를 가진다.

(방향 좌표 + 위치(x, y)좌표?)

따라서 각각의 이미지는 고차원 공간에 임베딩된 3차원 manifold 안에 존재한다고 볼 수 있다.

물체의 위치, 방향과 픽셀간의 복잡성으로 인해 이 manifold는 매우 비선형적일 것이라 추측할 수 있다.

입력값으로 이미지를 받아 위치에 상관 없이 사물의 방향을 결과값으로 내놓고자 한다면 중요한 차원은 오직 하나가 된다.