[PRML] 1.5 Decision Theory

1.5 Decision Theory

 

1.2장에서 확률론이 불확실성을 정량화하고 다루는 데에 있어 일관적인 framework를 제공한다는 것을 배웠다.

이 장에서는 확률론과 함께 불확실성이 개입된 상황에서 최적의 결정을 내리도록 하는 결정 이론에 대해 공부할 것이다.

 

입력 벡터 $\mathbb{x}$와 상응하는 타겟 벡터 $\mathbb{t}$(클래스 라벨)가 주어졌을 때 이를 이용해 새로운 입력 벡터 $\mathbb{x}_{new}$에 대해 예측 $\mathbb{t}_{new}$을 하는 모델을 만들고자 한다고 한다.

 

결합 확률(joint distribution) $p(\mathbb{x}, \mathbb{t})$는 이 변수들에 연관된 불확실성에 대한 완전한 요약을 제공한다.

학습 데이터로부터 $p(\mathbb{x}, \mathbb{t})$를 도출해내는 과정은 추론(inference)의 과정이며 이 책의 대부분을 구성하는 어려운 문제이다.

그러나 현실 세계에서 우리는 $t$의 값에 대한 구체적인 예측을 하거나, 보다 일반적으로 $t$가 가질법한 값에 기반하여 특정한 행동을 취해야 한다. 이것이 결정 이론이 다루는 주제이다.

 

예를 들어, X-ray 이미지로부터 환자가 암이 있는지 여부를 판단하려는 문제를 가지고 있다고 하자.

이 경우 $\mathbb{x}$ 는 X-ray이미지의 각 픽셀이며 $t$는 환자가 암이 있는지 여부이다.

• $t$가 $C_1$ 클래스에 해당될 경우 암이 있고, $C_2$ 클래스에 해당될 경우 암이 없다
• 구하고자 하는 확률은 $p(C_k|\mathbb{x})$이다.

 

베이즈 정리를 이용해 다음과 같이 나타낼 수 있다.

 

$p(C_k | \mathbb{x}) = \frac{p(\mathbb{x}|C_k)p(C_k)}{p(\mathbb{x})}$

 

여기에서 $p(C_k)$를 사전 확률로, $p(C_k|\mathbb{x})$를 사후 확률로 이해할 수 있다.

우리의 목적이 $\mathbb{x}$를 틀린 클래스에 배정하는 경우를 최소화하는 것이라면, 직관적으로 높은 사후확률을 갖는 클래스를 선택하게 될 것이다.

 

1.5.1 Minimizing the misclassification rate

우리의 목적이 오분류를 최소화하는 것이라고 하자.

우리는 각 데이터포인트 $\mathbb{x}$를 가능한 클래스 중의 하나로 배정할 규칙이 필요하다.

그러한 규칙은 입력 공간을 $\mathcal{R}_k$로 나누게 되는데, 이를 결정 영역(decision region)이라고 한다.

각 결정 영역 $\mathcal{R}_k$에 속한 데이터 포인트들은 모두 클래스 $\mathcal{C_k}$에 배정되게 된다.

결정 영역 사이의 경계선을 결정 경계(decision boundary, decision surface)라고 한다.

 

위와 같이 정의했을 때 앞서의 암 문제가 오분류될 확률을 다음과 같이 쓸 수 있다.

 

$\begin{align}p(\textit{mistake}) &= p(\mathbb{x} \in \mathcal{R}_1, \mathcal{C}_2) + p(\mathbb{x} \in \mathcal{R}_2, \mathcal{C}_1)\\&=\int_{\mathcal{R}_1}p(\mathbb{x}, \mathcal{C}_2) d\mathbb{x} + \int_{\mathcal{R}_2} p(\mathbb{x}, \mathcal{C}_1) d\mathbb{x}\end{align}$

 

$p(\textit{mistake})$를 최소화하는 방향으로 $\mathbb{x}$를 각 클래스에 배정하는 것이 최적의 방법이 될 것이다.

 

 

Figure 1.24 결정 경계

 

조금 더 일반적인 다중 클래스 문제의 경우, 오분류하게 될 확률을 계산하는 것보다 옳게 분류할 확률을 계산하는 것이 조금 더 쉽다.

 

$\begin{align}p(\textit{correct}) &= \sum_{k=1}^K p(\mathbb{x} \in \mathcal{R}_k, \mathcal{C}_k)\\&=\sum_{k=1}^K \int_{\mathcal{R}_k} p(\mathbb{x}, \mathcal{C}_k) d\mathbb{x}\end{align}$

 

 

1.5.2 Minimizing the expected loss

많은 경우에서 우리의 목적은 단순히 오분류되는 개수를 줄이는 것보다는 조금 더 복잡하다.

암 진단 문제를 다시 생각해 보자.

암이 없는 환자를 암이라고 판정하는 것보다는 암이 있는 환자를 건강하다고 판정하는 것이 훨씬 더 심각한 문제를 초래할 수 있다.

따라서, 첫 번째 경우가 조금 더 많아지더라도 두 번째 경우를 줄이는 것이 중요할 것이다.

 

이러한 문제를 손실 함수(loss function, cost function)를 도입함으로써 일부 해소할 수 있다.

손실 함수는 가능한 결정이나 행동을 취했을 때 발생하는 손실을 측정한 함수이다.

클래스 $\mathcal{C}_j$에 속하는 값 $\mathbb{x}$이 잘못된 클래스 $\mathcal{C}_j$에 배정되었을 때 발생하는 손실을 $L_{kj}$라고 하자.

모든 $k, j$에 관한 손실 $L_{kj}$을 모아 행렬로 만든 것을 손실 행렬(loss matrix)이라고 정의할 수 있다.

손실 행렬을 이용해 손실을 정확히 측정할 수 있지만, 이를 위해서는 새로운 값이 속하는 클래스를 알아야 한다.

하지만 일반적으로 이는 알려지지 않은 값이므로, 실제로는 평균 손실을 최소화하는 방법을 취하게 된다.

즉, 다음을 최소화한다.

 

$\mathbb{E}[L] = \sum_{k}\sum_{j} \int_{\mathcal{R}_j}L_{kj}p(\mathbb{x}, \mathcal{C}_k) d \mathbb{x}$

 

새로운 데이터 포인트 $x$에 대해 우리의 목표는 위 식을 최소화하는 $\mathcal{R}_j$를 구하는 것이다.

즉, $\sum_{k} L_{kj} p(\mathbb{x}, \mathcal{C_K}) d\mathbb{x}$를 최소화하는 $j$를 구해야 한다.

 

1.5.3 The reject option

 

사후 확률 $p(\mathcal{C}_k | \mathbb{x})$ 또는 결합 확률 $p(\mathbb{x}, \mathcal{C}_k)$이 1보다 현저히 작을 때는 분류 오류가 자주 일어난다.

이러한 범위에 속하는 $\mathbb{x}$에 대해서는 분류를 보류하는 것이 더 적절할 수 있다.

이러한 결정 보류를 거부 옵션(reject option)이라고 한다.

예컨대 앞서 살펴보았던 암 진단 예시에의 경우, 거부 옵션을 적용하면 이런 모호한 $\mathbb{x}$에 대해서는 판단을 보류하고 인간 전문가에게 판단을 맡기게 된다.

그림 1.26과 같이 임계치(threshold) $\theta$ 를 설정하고, $p(\mathcal{C}_k|\mathbb{x})$의 최대값이 $\theta$보다 작거나 같은 경우 해당 입력값 $\mathbb{x}$에 대한 판단을 보류한다.

만약 $\theta=1$로 설정한다면 모든 입력 데이터는 거부될 것이다.

또 $K$개의 클래스에 대해 분류 작업을 한다면 임계치를 $\theta < 1/K$로 설정함으로써 어떤 입력 데이터도 거부되지 않도록 할 수 있다.

즉, 거부되는 데이터의 개수는 $\theta$의 값에 따라 조절된다.

 

Figure 1.26 reject option

 

1.5.4 Inference and decision

지금까지 우리는 분류 문제를 추론(inference)와 결정(decision) 두 단계로 나누었다.

inference 단계에서는 학습 데이터를 통해 모델을 학습해, $p(\mathcal{C}_k|mathbb{x})$ 를 구했고,

decision 단계에서는 앞서 구한 사후 확률을 통회 최적의 클래스 배정 과제를 수행했다.

 

두 문제를 결합해 $\mathbb{x}$를 바로 결정으로 매핑하는 함수를 학습하는 것이 하나의 대안적 가능성이 될 수 있다.

이를 discriminant function이라 한다.

 

클래스 판별 문제들을 위 세 가지 방법으로 나눌 수 있다. 복잡도에 대해 내림차순으로 나열하면 다음과 같다.

 

• Generative models
  • 각 클래스 $\mathcal{C_k}$에 대해서 클래스-조건부 확률 $p(\mathbb{x}|\mathcal{C}_k)$을 추론한다.또한, 클래스 $\mathcal{C_k}$의 사전 확률인 $p(\mathcal{C_k})$를 추론한다.
  • 베이즈 정리를 사용해 다음과 같이 사후 확률 $p(\mathcal{C}_k|\mathbb{x})$를 얻는다.
    • $\begin{align}p(\mathcal{C}_k|\mathbb{x}) = \frac{p(\mathbb{x}|\mathcal{C}_k)p(\mathcal{C}_k)}{p(\mathbb{x})}\end{align}$
    • $\begin{align}p(\mathbb{x}) =\sum_k p(\mathbb{x}|\mathcal{C}_k)p(\mathcal{C}_k)\end{align}$
  • 사후 확률을 찾음으로써, 결정 이론을 이용해 새로운 입력값 $\mathbb{x}$이 속하는 클래스를 결정할 수 있다.
  • 이렇게 명시적, 혹은 내재적으로 입력, 출력 데이터의 확률 분포를 모델링하는 방법을 generative model이라고 한다.
    • 모델링된 분포로부터 새로운 샘플들을 생설할 수 있기 떄문에 generative 라는 이름이 붙었다.

 

• Discriminative models
  • 사후 확률 $p(\mathcal{C}_k|\mathbb{x})$를 직접적으로 추론한다.
  • 추론한 확률과 결정 이론을 통해 새로운 입력값 $\mathbb{x}$가 속하는 클래스를 결정한다.

 

• Discriminant functions
  • 입력 데이터 $\mathbb{x}$를 클래스 라벨로 매핑하는 discriminant function $f(\mathbb{x})$를 찾는다.
  • discriminant function 방식에서는 확률론이 사용되지 않는다.

소개된 세 가지 방법의 상대적인 장점을 생각해 보자.

generative model 방법은 $\mathbb{x}$와 $\mathcal{C}_k$에 대한 결합 확률분포(joint distribution)를 찾는 것이 포함되기 때문에 가장 까다로운 방법이다.

많은 경우에 $\mathbb{x}$는 고차원 데이터이고, 따라서 합리적인 정확도로 클래스-조건부 확률을 결정하기 위해서는 큰 학습 데이터셋이 필요할 수 있다.

클래스에 대한 사전 확률 $p(\mathcal{C}_k)$는 종종 학습 데이터셋의 클래스 분포에서 간단히 추론된다.

반면, generative model 방법의 장점은 $p(x)$를 추론하게 된다는 것이다.

이를 통해 모델에서 나타날 확률이 낮은 새로운 데이터 포인트를 탐지할 수 있다. (outlier detection, novelty detection)

 

generative model 방식은 결합 확률 $p(\mathbb{x}|\mathcal{C}_k)$를 찾아내기 위해 많은 자원과 학습 데이터를 요구한다.

그러나 분류 과제를 수행할 때 필요한 확률은 사실 $p(\mathcal{C}_k|\mathbb{x})$뿐이므로, generative model 방식보다는 $p(\mathcal{C}_k|\mathbb{x})$를 직접적으로 추론하는 discriminative model 방식이 더 적합할 수 있다.

그림 1.27에서 볼 수 있듯이, 클래스-조건부 밀도(왼쪽)은 사후 확률(오른쪽)에는 거의 영향을 끼치지 않는 많은 구조를 포함하고 있을 수 있다.

 

Figure 1.27

 

더 간단한 방식인 discriminant function방식은 그림 1.27의 초록색 경계선만을 찾아내는 방식이라고 생각할 수 있다.

그러나 discriminant function 방식을 사용할 경우 사후 확률  $p(\mathcal{C}_k|\mathbb{x})$에 대한 정보를 얻을 수 없다.

사후 확률에 대한 정보를 얻어야 할 이유는 다음과 같다.

 

• Minimizing Risk
  • 손실 매트릭스의 정보가 때때로 수정되는 경우를 생각해 보자.
  • 사후 확률을 알고 있는 경우 $\sum_{k} L_{kj} p(\mathbb{x}, \mathcal{C_K}) d\mathbb{x}$ 을 적절히 수정하여 결정 기준을 바꿀 수 있다.
  • 만약 판별 함수만 가지고 있는 경우, 새롭게 학습을 진행해야 한다.

 

• Reject option
  •  사후 확률을 통해 오분류 정도를 최소화할 수 있는 거부 옵션을 사용할 수 있다.

 

• Compensating for class priors
  • 학습 데이터가 심하게 불균형한 경우 학습하기가 쉽지 않다.
  • 각 클래스에서 같은 수의 데이터를 선택한 balanced data set 을 사용할 경우 보다 정확한 모델을 찾을 수 있다.
  • 이와 같이 학습 데이터를 수정한 경우 수정의 영향을 보상해야 한다.
  • 사후 확률은 사전 확률에 비례하기 때문에, 얻은 사후 확률에 $p(\mathcal{C}_k)$을 곱하고 정규화를 수행함으로써 사후 확률을 조정할 수 있다.

 

• Combining models
  • 복잡한 문제의 경우 여러 개의 간단한 문제로 나누어 해결하는 방식이 선호된다.
  • 각각의 모델이 사후 확률을 제공한다면, 그 확률들이 서로 독립적이라고 생각하고 다음과 같이 쓸 수 있다.
    • $p(\mathbb{x}_I, \mathbb{x}_B|\mathcal{C}_k) = p(\mathbb{x}_I | \mathcal{C_k})p(\mathbb{x}_B|\mathcal{C}_k)$
  • $\mathbb{x}_i$와 $\mathbb{x}_B$가 주어졌을 때의 사후 확률은 다음과 같이 주어진다.
    • $p(\mathcal{C}_k|\mathbb{x}_i, \mathbb{x}_B) \propto p(\mathbb{x}_I, \mathbb{x}_B|\mathcal{C}_k)p(\mathcal{C}_k) = \frac{p(\mathcal{C}_k|\mathbb{x}_I)p(\mathcal{C}_k|\mathbb{x}_B)}{p(\mathcal{C}_k)}$ 

 

1.5.5 Loss functions for regression

 

지금까지는 분류(classification) 문제를 위한 결정 이론을 살펴보았다.

이 장에서는 다항 곡선 피팅 문제와 같은 회귀(regression) 문제로 되돌아갈 것이다.

 

회귀 문제에서의 결정 단계는 입력값 $\mathbb{x}$과 타겟 벡터 $t$에 대한 예측값 $y(\mathbb{x})$을 결정하는 것이다.

먼저 회귀 문제에서의 손실 함수(loss function)를 $L(t, y(\mathbb{x}))$로 나타내면, 기대 손실(expected loss)는 다음과 같다.

 

$\mathbb{E}[L] = \int \int L(t, y(\mathbb{x})) p(\mathbb{x}, t) d \mathbb{x} dt$

 

회귀 문제에 있어 일반적인 손실 함수의 선택은 $L(t, y(\mathbb{x})) = \left\{ y(\mathbb{x}-t)\right\}^2$이다.

이 경우 기대 손실을 다음과 같이 쓸 수 있다.

 

$\mathbb{E}[L] = \int \int \left \{ y(\mathbb{x} - t)\right\}^2p(\mathbb{x}, t) d \mathbb{x} dt$

 

여기서의 목표는 $\mathbb{E}[L]$ 을 최소화하는 $y(\mathbb{x})$를 찾는 것이다.

만약 완벽히 flexible 한 함수 $y(\mathbb{x})$를 가정한다면, 다음과 같이 미분값이 0이 되도록 놓고 풀 수 있다.

 

$\frac{\delta \mathbb{E}[L] }{\delta y(\mathbb{x})} = 2 \int \left\{ y(\mathbb{x})-t\right\}p(\mathbb{x}, t) dt = 0$

 

$y(\mathbb{x})$에 대해 풀고, 합의 법칙과 곱의 법칙을 적용하면 다음 식을 얻는다.

 

$y(\mathbb{x}) = \frac{\int tp(\mathbb{x}, t) dt}{p(\mathbb{x})} = \int tp(t|\mathbb{x}) dt = \mathbb{E}_t[t|\mathbb{x}]$

 

이 식은 조건부 $x$에 대한 $t$의 평균과 같다.

 

 

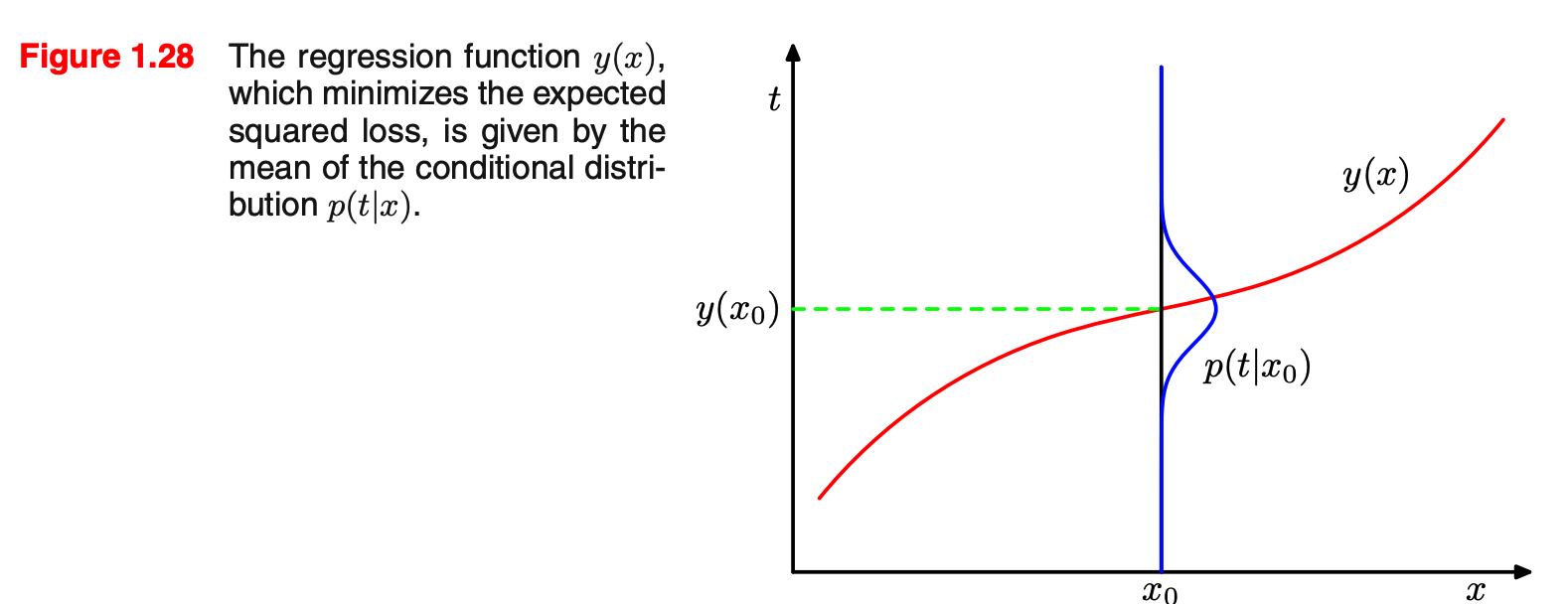
Figure 1.28 기대 손실을 최소화하는 회귀 함수

 

손실 함수의 구성에 대한 직관을 얻기 위해 다른 방식으로 접근해보도록 하자.

$\mathbb{E}[t|\mathbb{x}]$를 더하고 뺌으로써 손실 함수를 다음과 같이 다시 쓸 수 있다.

 

$\begin{align}\left\{ y(\mathbb{x}-t)\right\}^2 &= \left\{ y(\mathbb{x}) - \mathbb{E}[t|\mathbb{x}] + \mathbb{E}[t|\mathbb{x}]-t\right\}^2 \\ &= \left\{ y(\mathbb{x}) - \mathbb{E}[t|\mathbb{x}]\right\}^2 + 2\left\{y(\mathbb{x}-\mathbb{E}[t|\mathbb{x}])\right\}\left\{\mathbb{E}[t|\mathbb{x}]-t\right\} + \left\{\mathbb{E}[t|\mathbb{x}]-t\right\}^2\end{align}$

 

여기에 인테그랄을 취함으로써 중간 항들은 사라지고, 기대 손실을 다음과 같이 쓸 수 있다.

 

$\mathbb{E}[L] = \int \left\{ y(\mathbb{x}) - \mathbb{E}[t|\mathbb{x}]\right\}^2 p(\mathbb{x}) d\mathbb{x} + \int \left\{ \mathbb{E}[t|\mathbb{x}] - t\right\}^2 p(\mathbb{x})d\mathbb{x}$

 

위의 수식으로부터 기대 손실값을 두 가지 구성으로 나누어 볼 수 있다.

 

• 모델이 얼마나 샘플을 잘 나타내는지
• 샘플이 포함하는 노이즈가 어느 정도인지

후자의 요소가 모델과는 독립적인 요소이므로, 이는 더 이상 줄일 수 없는 최소 손실을 나타낸다.

 

분류 문제와 마찬가지로, 먼저 적절한 확률을 결정한 다음 그 확률을 사용해 최적의 결정을 내리거나, 직접적으로 결정을 내리는 모델을 설계할 수 있다.

이 방식들을 복잡도에 의해 내림차순으로 정리하면 다음과 같다.

 

• 결합 확률 $p(\mathbb{x}, t)$를 추론하고, 그로부터 조건부 밀도 $p(t|\mathbb{x})$를 구한다. 위의 방식을 사용하여 최종적으로 $y(\mathbb{x})$를 구한다.
• 조건부 밀도 $p(t|\mathbb{x})$를 직접 구하고 $y(\mathbb{x})$를 구한다.
• 학습 데이터로부터 $y(\mathbb{x})$를 직접 구한다.

---

우리는 계속 손실 함수로서 squared loss 함수를 사용하고 있지만, 다른 손실 함수를 사용하는 것도 가능하다.

Minkovski 손실 함수는 squared loss 손실 함수의 간단한 일반화로서, 기대 손실은 다음과 같이 주어진다.

 

$\mathbb{E}[L_q] = \int \int |y(\mathbb{x}) - t|^q p(\mathbb{x}, t) d\mathbb{x} dt$

 

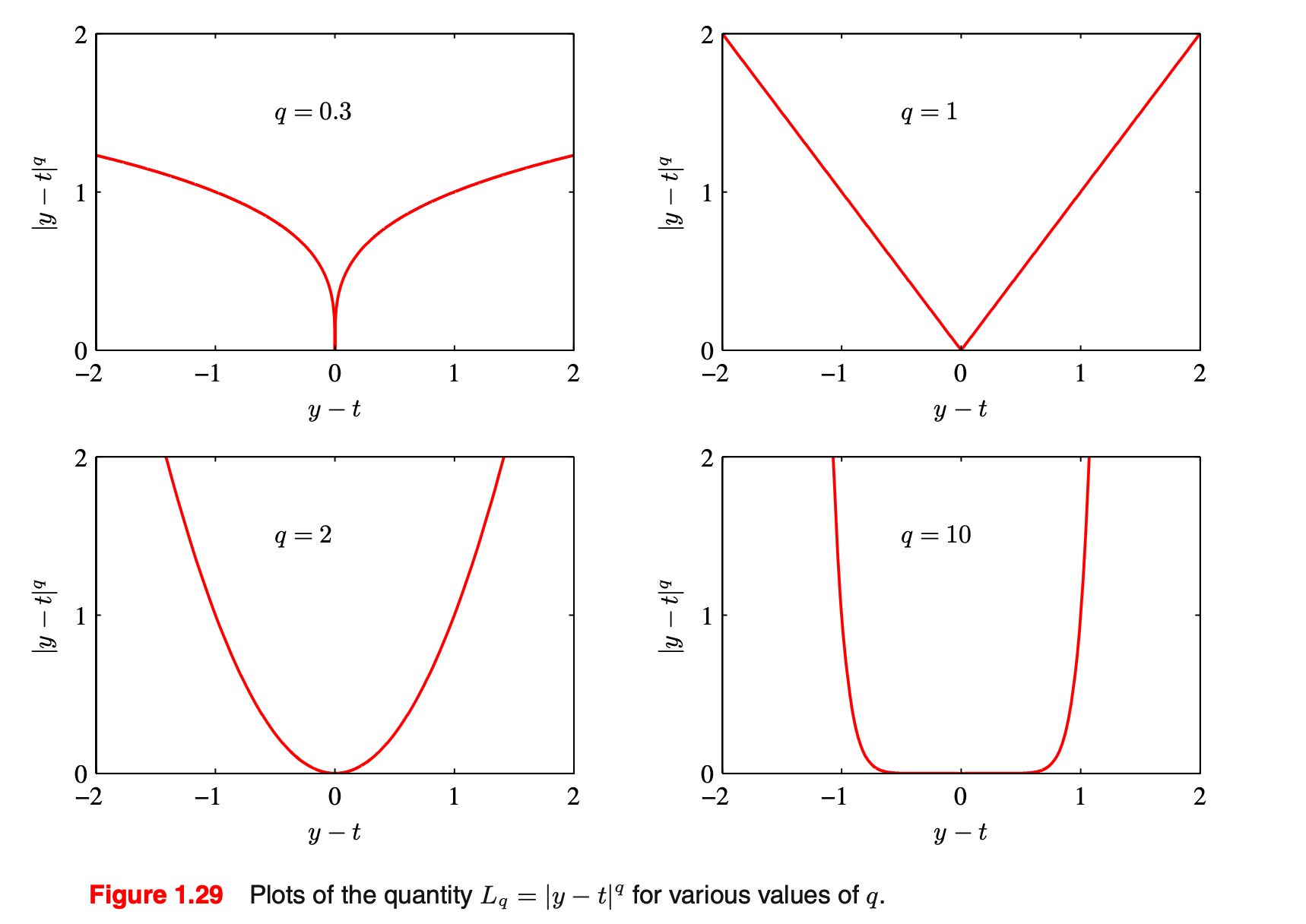
Figure 1.29 $q$의 값의 변화에 따른 손실 함수