-
[PRML] 1.1 Example: Polynomial Curve Fitting책 리딩/PRML 2020. 7. 12. 10:23
1.1 Example: Polynomial Curve Fitting
$f(x) = \sin (2 \pi x)$ 예측하기
문제 설정:
$\mathbb{x} = (x_1, \ldots, x_N)^T$: 인풋 벡터
$\mathbb{t} = (t_1, \ldots, t_N)^T$: 타겟 벡터 ($f(x) = \sin (2 \pi x)$ 로부터 관찰된 $y$값)

Figure 1.2 $sin(2 \pi x) 로부터 관측된 값들$ 목표: 트레이닝 셋을 잘 학습하여 새로운 데이터 $\hat{x}$가 주어졌을 때 예측치 $\hat{t}$를 생성하는 것
유한한+노이즈가 포함된 데이터셋으로부터 내재된 구조를 파악하는 것은 어렵다.
- 확률론(probability theory): 불확실성을 정확하고 정량적으로 표현하기 위한 프레임워크 제공
- 결정론(decision theory): 확률론을 이용하여 적절한 확률에 따른 최적의 예측을 할 수 있도록 함
이 장에서는 다음 다항식을 이용해 데이터를 학습해 볼 것이다.
$y(x, \mathbb{w}) = w_0 + w_1 x + w_2 x^2 + \ldots + w_Mx^M = \sum_{j=0}^M w_j x^j$
$M$: 다항식의 차수
$y(x, \mathbb{w})$는 $x$에 대해서는 비선형이고, $\mathbb{w}$에 대해서는 선형이다.
이와 같이 알려지지 않은(학습해야 할) 매개변수들에 대해 선형인 모델을 선형 모델(linear model)이라고 한다.
이 매개변수 $\mathbb{w}$의 값들을 다항식을 트레이닝 데이터에 대해 학습시키는 과정에서 정해진다.
에러 함수(error function): 주어진 $\mathbb{w}$와 학습 데이터셋에 대해 $y(x, \mathbb{w})$의 값과 실제값 사이의 차이를 측정하는 함수
가장 자주 쓰이는 에러 함수는 오차 제곱의 합(sum of the squares of the errors)이다.
($\frac{1}{2}$는 향후 계산의 편의를 위해 붙음)
$E(w) = \frac{1}{2} \sum_{n=1}^N \left\{ y(x_n, \mathbb{w}) - t_n\right\}^2$

Figure 1.3 오차 제곱의 합 학습 과정은 에러 함수를 최소화하는 $\mathbb{w}$를 찾아가는 과정이다.
오차 제곱의 합 에러 함수가 $\mathbb{w}$에 대한 이차 함수이기 때문에,
에러 함수의 도함수는 $\mathbb{w}$에 대한 선형 함수가 된다.
따라서 에러 함수가 최소값을 갖게 하는 $\mathbb{w}$의 값은 유일하며, 이를 $\mathbb{w}^*$ 라고 할수 있다.
다항식의 차수 $M$을 선택하는 문제는 model comparison, model selection이라고도 불리는 문제의 한 예이다.
그림 1.4의 $M=0,1$ 과 같이 트레이닝 데이터에 비해 모델이 너무 단순하면 과소적합(under-fitting)문제가 발생한다.
그림 1.4의 $M=9$ 에서와 같이 트레이닝 데이터에 대해서는 완벽하게 학습되었지만 데이터에 내재된 구조를 찾아내는 데 실패한 경우를 과적합(over-fitting)이라고 한다.

Figure 1.4 차수에 따른 다항식 학습의 결과 각 모델에 대한 평가를 하기 위해 RMS(Root Mean Squared) 에러 함수가 사용된다.
$E_{\textit{RMS}} = \sqrt{2E(\mathbb{w}^*)/N}$
이 때 전체를 $N$으로 나눔으로써 서로 다른 크기의 데이터셋을 같은 기준으로 비교할 수 있다.
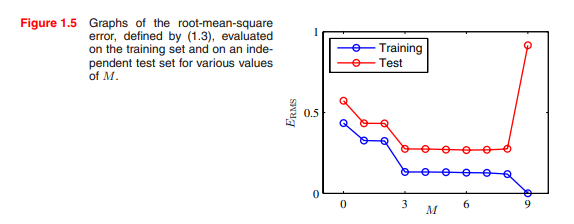
Figure 1.5 차수에 따른 RMS의 변화 모델의 복잡도가 같을 때 주어진 데이터의 개수에 따라서도 결과가 달라진다.
그림 1.6의 왼쪽을 보면 $N=15$일 때 오버피팅이 발생하지만 오른쪽의 경우 $N=100$으로 크지만 오버피팅이 발생하지 않는다.
즉 큰 데이터셋을 가지고 있으면 오버피팅 문제를 어느 정도 피할 수 있다.

#B47EDEFigure 1.6 데이터 개수에 따른 학습의 변화 여기에서 도출되는 거친 휴리스틱은 파라미터의 개수가 가진 데이터의 개수의 상수배($\frac{1}{5}$, $\frac{1}{10}$등) 이하여야 한다는 것이다.
그러나 파라미터의 개수가 복잡도를 결정하는 데 항상 가장 중요한 지표는 아니고,
데이터의 개수보다는 풀고자 하는 문제의 복잡도에 모델의 복잡도를 맞추는 것이 더 합리적인 방향으로 보인다.
추후에 maximum likelihood와 Baysian 방법을 통해 이를 좀 더 살펴볼 것이다.
이 챕터에서는 지금과 같은 접근법으로 오버피팅 문제를 해소하는 법을 알아보겠다.
정규화(Reularization)방법은 파라미터들이 너무 큰 값을 갖지 못하도록 에러 함수에 페널티를 주는 항을 하나 추가함으로써 동작한다.
$\tilde{E}(\mathbb{w}) = \frac{1}{2} \sum_{n=1}^N \left\{ y(x_n, \mathbb{w}-t_n)\right\}^2 + \frac{\lambda}{2}\lVert w \rVert^2$,
여기에서 $\lVert w \rVert^2 = w_0^2 + \ldots + w_M^2$이고, 정규화 계수(regularization coefficient) $\lambda$는 정규화 항의 상대적 중요도를 나타낸다.
정규화 항을 추가해도 에러 함수는 $\mathbb{w}$에 대해서 닫힌 형태 (유일해를 구할 수 있는 형태)를 유지하게 된다.
그림 1.7의 왼쪽과 같이 적절한 정규화 계수를 주었을 경우 오버피팅을 막을 수 있다.
그러나 그림 1.7의 오른쪽과 같이 정규화 계수가 너무 커질 경우, 오히려 언더피팅이 발생할 수 있다.

Figure 1.7 정규화 계수에 따른 모델 변화 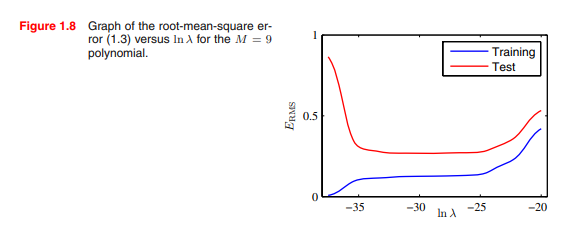
Figure 1.8 정규화 계수에 따른 RMS 변화 '책 리딩 > PRML' 카테고리의 다른 글
[PRML] 1.6 Information Theory (작성중) (0) 2020.07.12 [PRML] 1.5 Decision Theory (0) 2020.07.12 [PRML] 1.4 The Curse of Dimensionality (0) 2020.07.12 [PRML] 1.3 Model Selection (0) 2020.07.12 [PRML] 1. Introduction (0) 2020.07.11